When comparing how different regions have been impacted by the coronavirus over time, it is important to define a “starting point”: an early timepoint in the spread of the virus from which the timepoints of future observations can be measured. Although one may think that the natural place to start would be a region’s first recorded COVID case or the first COVID fatality, this can lead to improper or uninformative region-to-region comparisons. Testing at the beginning of a local COVID outbreak can be seriously unreliable, and the spread of the disease from the first handful of cases to the next is tied to the idiosyncrasies of people’s daily behaviors.
In New York state, where COVID may have arrived more than one month before the first confirmed case on March 1, 2020, confirmed fatalities soared from 1 death to nearly 500 in just two weeks. Conversely, the Norfolk-Newport News area of Virginia had still not witnessed ten deaths one month after its first.
COVID metrics between different afflicted regions appear to begin behaving in a more predictable manner once the disease has reached a critical mass and begun spreading widely. COVID data analysts try to set the starting point for their measurements at some level where this critical mass has likely been reached and the initial random variation has dissipated.
Different modelers will choose different thresholds. The Financial Times measures new cases or deaths by country from the day 10 cases/day or 3 deaths/day was reached, and cumulative cases/deaths from the day of the 100th case or death. The data visualization at 91-divoc.com measures by nation from the day of the 100th case or the 10th death; for regions, it starts at 20 cases or 5 deaths.
What threshold makes the most sense?
In our analysis, we examined the Johns Hopkins CSSE time series dataset (up to 5/31/20) to determine how varying the choice of starting point affects the precision of forecasts. We chose to analyze counts of confirmed COVID fatalities, which are more reliable early-stage figures than confirmed COVID cases. (However, deaths always lag cases by up to two weeks.)
First, we grouped U.S. county-level COVID death counts into the top 100 most populous Census metropolitan statistical areas (MSAs), which adhere to county boundaries. By population, the largest of these is New York-Newark-Jersey City and the smallest is Chattanooga.
Next, we shifted the daily figures for the MSAs to synchronize the two weeks before and two weeks after the day X total deaths was reached, where X = 1, 2, 5, 10, 20, 50, 100, 200, 500, 1,000, and 2,000.
(Why these amounts? Contagions spread exponentially, and these numbers break the span from 1 to 2,000 into roughly equal logarithmic intervals. As of today, only three MSAs have reached 5,000 total deaths. And why two weeks? That is roughly the duration of a COVID infection.)
To determine the efficacy of each threshold of X, we created regressions for the “before” and “after” weeks, based on the linear formula and its exponential transformation shown below:
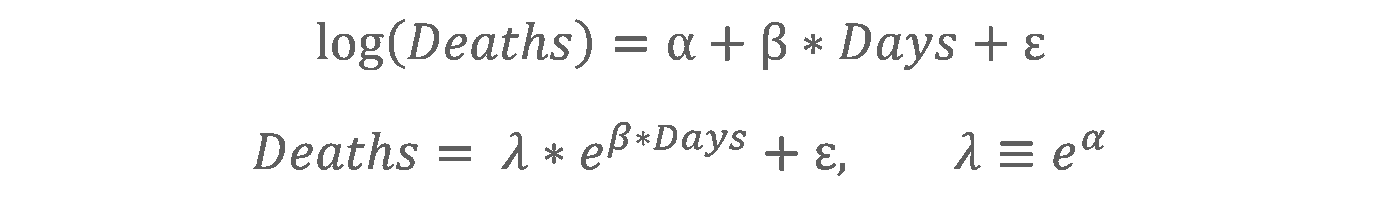
(Here, α and β are the y-intercept and slope of the regression and ε is the residual error.)
Below in Chart 1, see an interactive graph illustrating the data for X = 1 death (the day of the first recorded COVID death in each MSA).
Chart 1. Rendered in R, ggplot2, and Plotly. Hover over points to see more information.
When X = 1, the trajectories on the right (after) side of the graph diverge widely, signifying that this observation point occurs too early in the spread of the virus to meaningfully predict or compare trajectories. Additionally, for this and the next few values of X, any data that would appear on the left (before) side of the graph are inscrutable, since counts of zero deaths have an infinitesimal logarithmic value and must therefore be discarded.
When moving to higher thresholds of X, we are able to see the trajectories on the after side begin to coalesce and the data on the before side start to grow. For the highest X, few MSAs have yet reached those death counts, so the trajectories on both sides of the graph are much fewer in number. Here are selected values of X, visualized:
Charts 2-4. Rendered in R, ggplot2, and Plotly. Hover over points to see more information.
Across all these test values of X, the mean square error (MSE) of the observations to the before and after regression lines is what attracts our attention, more so than the regressions themselves. The MSE allows us to understand how closely the trajectories coalesce around the regression line, and thus around each other. A low MSE implies that the observations fit well around the line, indicating better predictability. For the first few values of X, the MSE is lower on the before side than on the after side. For larger X, the opposite is true: the after MSE is lower and the before MSE is higher.
As X increases, the point at which the after MSE becomes less than the before MSE is where the near future becomes more predictable than the near past. In our data, this point occurs just shy of X = 50, as visualized in the graph below:
Chart 5. Mean square error for each value of X.
The data shown in this graphic imply that the fatality trajectories have lost most of their early-stage variability around the time of the 50th death. After reaching this threshold, the trajectories behave more consistently — not totally in lockstep, in fact far from it, but more consistently than at any point before.
The widening difference between the before and after MSE curves beyond X = 50 indicates that 100, 200, or 500 might be even better thresholds, but we must bear in mind the passage of time. The higher we set X as the starting point, the more precision we gain in modeling the future, but the more data we are willingly discarding. We should not choose a starting point so late in the outbreak that we end up ignoring weeks of mid-phase growth in the fatality count for the sake of a more precise model.
The steep decline in both MSE curves at X = 1,000 and 2,000 is an artifact of the rarity of those high death counts as of this month (June); data is simply too scarce for these X. If more regions across the U.S. were suffering COVID fatality rates that severe, we could expect to see the before MSE curve trend further and further upwards.
What we can learn
This analysis shows how the growth in COVID fatalities in U.S. urban regions reaches a “critical mass” and loses its early-stage variability at some time around the 50th death. Graphing MSE shows that setting a higher starting point for measurements enables greater precision, but this comes with the price of discarding informative data.
This is an important finding for comparative analysis and future COVID time-series data visualizations. Yet, we must caution against overstating the rigor of this analysis. We are not epidemiologists and this is not a professional epidemiological study. We have regressed over the variable of time but not over variables of human behavior or system factors. Hopefully this analysis, albeit rough, can impart some mathematical basis to the assumptions underlying future analysis.
Download our data tables for this post here.